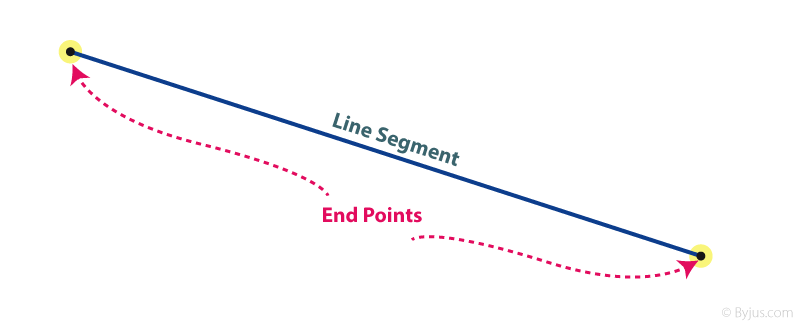
A line segment is a fundamental geometric concept, representing a part of a line that is bound by two distinct endpoints. In the context of everyday shapes and figures, line segments serve as the building blocks for more complex structures, such as polygons, triangles, and other multi-sided shapes. Unlike a line, which extends infinitely in both directions, a line segment has a measurable length and a definite endpoint at each of its extremities. The importance of understanding line segments lies in their contribution to the formation of various geometric shapes and the ability to measure their specific lengths.
 |
| byjus.com |
When we delve into the concept of a ray, we encounter a unique element that combines attributes of both a line and a line segment. A ray, much like a line, extends infinitely in one direction, yet it possesses an endpoint at the other end. This non-terminating nature of a ray results in the inability to measure its length. Represented with an arrow pointing in the direction of its infinite extension, a ray is identifiable by its starting point and the open-endedness on the opposite side. While a line segment can be precisely measured due to its two distinct endpoints, a ray's infinite extension precludes any such measurement.
Differentiating between a line segment and a ray highlights their inherent distinctions. A line segment, with its two finite endpoints, allows for the precise calculation of its length. In contrast, a ray features one fixed endpoint and an unbounded extension in the opposite direction, making the measurement of its length impossible. Moreover, a line lacks any endpoints and extends indefinitely in both directions, setting it apart from both line segments and rays. This distinction emphasizes the role of endpoints in determining the nature of these geometric elements, with a line segment having two endpoints, a ray having one, and a line having none.
 |
| byjus.com |
Furthermore, the immutability of a line segment's length is a key characteristic that sets it apart from a line. While a line can be extended infinitely in both directions, a line segment's endpoints limit its length to a definite measure, establishing its significance in the construction of specific shapes and figures. Additionally, the unidirectional extension of a ray exemplifies its unique property, differentiating it from a line segment and a line. Understanding the distinctions between these geometric components is essential for comprehending their applications in various mathematical and real-world contexts.
In summary, the comprehension of line segments and rays is vital for grasping the construction of geometric shapes and figures. While a line segment constitutes a measurable part of a line with two endpoints, a ray combines elements of a line and a line segment, extending infinitely in one direction and featuring a single endpoint. These fundamental concepts lay the groundwork for further exploration into the intricacies of geometry, aiding in the comprehensive understanding of shapes and their properties.



